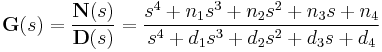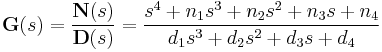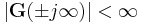Proper transfer function

In control theory, a proper transfer function is a transfer function in which the degree of the numerator does not exceed the degree of the denominator.

Example

The following transfer function is proper

\textbf{G}(s) = \frac{\textbf{N}(s)}{\textbf{D}(s)} = \frac{s^{4} %2B n_{1}s^{3} %2B n_{2}s^{2} %2B n_{3}s %2B n_{4}}{s^{4} %2B d_{1}s^{3} %2B d_{2}s^{2} %2B d_{3}s %2B d_{4}}

because

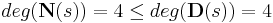deg(\textbf{N}(s)) = 4 \leq deg(\textbf{D}(s)) = 4 .

The following transfer function however, is not proper

\textbf{G}(s) = \frac{\textbf{N}(s)}{\textbf{D}(s)} = \frac{s^{4} %2B n_{1}s^{3} %2B n_{2}s^{2} %2B n_{3}s %2B n_{4}}{d_{1}s^{3} %2B d_{2}s^{2} %2B d_{3}s %2B d_{4}}

because

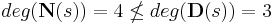deg(\textbf{N}(s)) = 4 \nleq deg(\textbf{D}(s)) = 3 .

Implications

A proper transfer function will never grow unbounded as the frequency approaches infinity.

|\textbf{G}(\pm j\infty)| < \infty

See also